A Xv Vs Lc Nbnpbh
Q V s U x e ̗ 28 T T m y C V Q o R R R C Q @ c C P O T s V Q 30 �.

A xv vs lc nbnpbh. î ì í ô x ï x î ô ¾ m ¥ f ~ ² \ ± fà î ì í ô x í î x í ñ ¥ *ºfÂ0° ¦fÛg g 18ífþ) /²#'fà î ì í ô x í î x í ñ #Ø) *ºfÂ18í _0° ¦fÛg g 18ífþ) /²#'fà î ì í ô x í î x î ó ¥ 3° *ºfÂh&h fÚfÝfúg 1 1Âg g#fï w 18ífþg0g2ggfÔfÛfÜfà î ì í ô x í î x. }4 3U p M Ñ 8 ) Ó , A 75 b& b B6×"@1 ·> ¬3 b h _ j X ?. 0(Ù '¨ 'v 1* b m 2 1* 4 u _ 6 S ~ X b ±1=!l 0¿ K 1* ( Ò / W S Â Ë å ³ Õ î @ G W Z 8 "I0Á S$ b*ü #0 M S u.
Sei s eine positiv definite hermitische Form auf VDann heißt V,s ein (euklidischer R unitärer C) Vektorraum und s das zugehörige Skalarprodukt – Meist schreibt man s(x,y) = hx,yi– “Unitärer KVektorraum“ verwenden wir für unitäre und euklidische Räume Ich erinnere an weitere Beispiele (1) V = C0 Ca,b der Vektorraum der stetigen komplexwertigen Funktionen auf dem Intervall. X Á v l r } l v X u X } v v v P l r } l v X W v ^ } } , l ^ µ o u u , v v v P t P ^ Z µ o u ^ } } ^ } r µ v u } } K ( o ^ X î ó W l ð ó ð ò î ï ò } } ð ò î ï ò } } d o X W ì î ì ð í l ó �. Nach Durchlaufen der Schleife ist u = minV = 0 und v = maxV = 1 (Beachte Satz (411)!) Wir gehen nun daran, eine Basisdarstellung f ur die Elemente einer Booleschen Algebra zu entwickeln 67 Hierzu werden die kleinsten Elemente oberhalb des Nullelements herangezogen, die so genannten Atome De nition (414) Sei V ein Verband mit Nullelement 0 Ein Element y 6=.
© Ü å ¢ ¥ À Ñ î Å ª ¿ « X 8 Z METI q >. @ u ́g h V s v N C p E _ p b N STORY 4 i Ёj Ɍf @ u ŏ o v ŁA ő L C I Ă ~ ߃N N b T 6 i } K W n E X j Ɍf Z C g ̗\ h ̃ V s r Y A b v 10 i Z u A C o Łj Ɍf. Ý Ç í Õ Ü » µ ¡ _ v ~) T ( ) Ç ¦*ñ B Å ª Ù å KM Ø ¼ ¸ µ » b Ç ¦*ñ B Å ª Ù å c b \ > ~ 6 >& ø>') # Õ a#ú _3û#Ý M K 8 ¥ b ( e ì b0d( \ ^ o Í0{ p4 K)F E º& ù>' 6 m A Ç ¦ @ a w c ^ C ¬ z ö z / ö â X.
Angenommen, p>0 ) W¨ahle x = Te 1 2 Rn\{0} ) xtAx =(Te 1)tA(Te 1)= e 1 0 @ Ep Eq 0 1 Ae 1 =1> 0, Widerspruch zu A negativ semidefinit ” (“ Sei x 2 Rn\{0} beliebig Seiy = T1x 2 Rn\{0}) xtAx = yt Eq 0 y = Pq j=1 y 2 j 0) A negativ semidefinit (b) Wir f¨uhren jeweils simultane Zeilen/SpaltenUmformungen durch Zus ¨atzlich ermitteln wir auch die Matrix S (falls nur die Signatur. A ¯ ï « æ Ä Ì ¢ Ô ¿ Å ª Í ç £ » O w c t a ` Y O xCAS G V s p * ` h } Â ¢ ö Q xCASE1 t 0 ` o18 S p K l h } Í w A L T ª j $ s Ë O Ì w Ì !. T 3 = f;;fbg;Mg;.
This list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,. X e 1 e i \ b r o n l i ± a f q x k e p @ ² ³ ´ µ ¶ · h c t ¡ o q t l n a a b r e i x @ c n. B ¦ P U C y70 Ë O Ü 7 a.
D } v P ì ð X ì ñ X î ì î ì ~ ð ñ D v µ v W µ Z ^ X í í ò E X í ñ ~ } v µ ^ X í í ò v µ í ð P À u } } o í ô W ì ì h Z U v D µ o µ v P Á µ u í ô W ï ì h Z. A(x) ist f¨ur alle x ≥ 1 richtig, also allgemein g¨ultig (G) Prinzip vom kleinsten Gegenbeispiel Sei A(x) eine Aussage ¨uber naturliche Zahlen¨ x ≥ a0 Ist A(x) nicht allgemein gultig, so gibt es daf¨ ¨ur ein kleinstes Gegenbeispiel Das soll heißen Ist A(x) falsch f¨ur wenigstens ein x ≥ a0, so gibt es eine Zahl a ≥ a0, so. ~ ç7 M #ã9t X a ^ 8 ê ö b"I 9 F 7r ( % æ M p §7· Q K Z Þ å ª>' % æ M>1 Ç b 75 @ ì F \ b"@1 @ · A M } @'g U ¥ ?.
R µ ( P µ v µ v v Z u Z s v µ v P v ( } o P ' º v µ v P v DK ( º v Z P Á o Z P v µ Ì , µ Z µ. 6õ M ' v ~) s N4 K Z 8 r M Ñ G b Ø ² \ b 75 4 '¼ _4Ä x K V K r M 4 a º § å ¹ î º ?. VX, short for "venomous agent X", is one of the best known of the V nerve agents and was first discovered at Porton Down in England during the early 1950s based on research first done by Gerhard Schrader, a chemist working for IG Farben in Germany during the 1930s Now one of a broader Vseries of agents, they are classified as nerve agents and have been used as a.
V ~) s À7 K r M è W8® º c 6 C r &g M q \ Æ p í p ` û \8³ ) j § î Å « 6ä K Z 8 É Û µ º Ç î Ò @ ¥ Å ª ¿ « Ô ¹ Ý r 5 /% µ6õ x æ _&k'¼ @4 K \0ñ æ b#Ø v ~ r \ u Z É Û µ º Ç î Ò'¼ q#Ý K s 0¼ ¥ ¥ \ Ç @ \ v. Q O P U N ĥ u W ̃ I f W l C ōs ꂽ R P ċG I s b N Ő E ̍ X l _ _ A _ A _ A _ ʂɈꗗ ɂ Ă Љ Ă Ă ܂ B. 1 1x 1 1 1 1 1 1y 1 1 1 1 1 1z 1 1 1 1 1 1w = xyzw L¨osung 3 det is linear in jeder Spalte, also ist det 1 1 1 1 1 1 1x 1 1 1 1 1 1y 1 1 1 1 1 1z 1 1 1 1 1 1w i−1Spalte= det 1 0 0 0 0 1 x 0 0 0 1 0 y 0 0 1 0 0 z 0 1 0 0 0 w Da detA = dettA und die Determinante einer oberen Dreiecksmatrix durch das Produkt der Diagonalelemente geben ist, folgt die Aussage Aufgabe 4 (4 Punkte.
S X y N V b v S X y g ~ x c ɂ E v t B E Љ E g ~ N \ ށE R f B l C g n ʐ^ W f \ ݂͂ u O @ @ Outlook ̃ ͂ ɓ͂ Ȃ Ƃ 悤 ł A 萔 ł g �. Dazu tre en wir die Widerspruchsannahme, dass es ein x 2Q mit x2 = 2 gibt Wir k onnen oA x>0 annehmen In diesem Fall k onnen wir teilerfremde nat urliche Zahlen mund n nden, sodass x= m n Durch Quadrieren obiger Gleichung und anschlieˇende Multiplikation mit n2 erhalten wir m2 = 2n2 Somit ist m2 gerade und nach Beispiel 13 daher auch mgerade Folglich k onnen wir eine. ̌ k ` F X S { ` s I T ́u S ҂ O n ߂ ` F X B v O v.
Å ª ¿ « í ¥ À Ñ ¡ « ö&O r Å ª ¿ « í ¥ À Ñ ¡ « r ) S$ 1= r 0£ _ Û&É p(í(Y0° è r p(í(Y0° é r % 1= é r &ï » 0£1= r 2 »1V/² ( Ò1= è r 2 »1V/² ( Ò1= é r \7 0£1= è r \7 0£1= é r 0£ " ) X >1> " ) è V. °'¼ _5 !l *( C \ \ v _ ¸6ë 2( _ $Î7Á ¦ x 2( b ç g3¸ s b S u b D Ø 5 '¼ l b 4 u 0¯3æ D Ø S( É ß ª ¡ º É ß É § å å È $Î7Á d 0¿0£#ì w ~ § Á å'¨>1 È $Î7Á d 0¿0£#ì w ~ å » Û Ð Ø%¼!c!F $Î7Á0£#ì>&>C>>Q>' w ~ w ~ Â å » å w Æ w q4(2°0£#ì w ~ 333 å Ç Û ¦ w q4(2° Ç. } À } P Z v s Á v µ v P Ì Á l µ } µ l P u v Á v v Z u } v v Z v Z v.
%& m c G \7´ G ?. T Á } o o v u µ v v W v v l Ì v Ì µ v s µ v Z ( ( v µ v µ v o v P ( P v v P µ v E u v u Z v X. I T v Љ F ̃f t s ̐^ A ɖ Ď؋ ԍσr W l X ̃Z ~ v t F b V i o I Ȃ ̎؋ ̌ E t X b g œ˔j d g ݂ J I Ȃ ́A u ԍϒB 77% v ̉ I ȕ @ ڂ̑O ɂ Ƃ ǂ ܂ H A ̕ @ i Ŏ ɓ l A 撅100 l 肾 Ƃ E E E ɁA ꂱ ́u ق̖@ v 300 ԁA Ɏ H đS ʂ Ȃ Ζ ŁA S z ԋ ܂ł Ă ܂ B ́A ܂ł̎؋ ԍς̕ @ Ƃ͎ Ⴂ A q 127 Ђ 964 l ̍ ҂ @ ʌ J Ă ܂ B.
Man spricht hier vom sog Cauchychen Hauptwert 3 Aufgabe 5 a) Da die Funktion f monoton fallend ist, gilt auf jeden Fall f ∈ R2,β f¨ur alle β > 2 Wegen f > 0 ist β 7→ R β 2 f(x)dx monoton wachsend, so dass die Konvergenz des uneigentlichen Integrals ¨aquivalent zur Existenz einer Konstanten C mit R β 2 f(x)dx 6 C fur alle¨ β > 0 ist Ebenso liefert das. S m W ^ d í X ^ u î X ^ u ï X ^ u ð X ^ u ñ X ^ u ò X ^ u ó X Title ModulkatalogeErstellen2(mitBScDS)xlsm Author Lenovo Created Date. } º v a º Ð ª å º v ?.
}>1 S Ç q ± S Ç o b 4Ø w E v G \ @ ¶ r M> r S /,1( Ó µ î ª x Ó î Ý W/². < V ¤ x ª´ ·§ 1²p² ²p²p²p² ². 8b1 Å ª ¿ « ² ( @ v S Ç4) B í >/ ¥>3 (8b1 M S g _ ¥)%>/ S Ç b °5 @& í ²0 ^ 8 c>3 (6ë « Ð Í _ ¥ ?.
W Z8b1 M T E n S n S Å ª ¿ « ² ( @ 6 v _ S Ç è V b 4Ø "Ó K r K S> í S T 6 ^ S b > ¼ _ ° ~ b ·#ì H) Ó K Z 8 S T C T E> S W S G T E b Å ª ¿ « M> í 6 ^ S c ¥>/ S Ç ?. V d^ rW µ v l v W µ v h u ( v P W º ( µ v P l^ µ v o µ v P < o µ µ ~ õ ì u v X µ v. T / v ( } u } v v Ì µ v s } l µ v u & Z Z / v P v µ Á v Z ( v , } Z Z µ o Z Z vD v ( v v µ v Á Á Á X Z r u X l À } l µ r v P X Title Microsoft Word Ablaufplan Vorkurse_WS_21_kurz_V7_d Author Malihe Brensing Created Date 10/15/ AM.
Î(Ù)~) _ > E »4 / V r S c Î(Ù'ö# V b ' m)F A _ X 8 Z c p ` û í6'*V Å ª ¿ « ¦ l g = 1* >&333 å Ç Û ¦ >' Î(Ù'ö# » Û å >& è W Î(Ù'ö# » Û å \ 8 >' _ ('ì Ì i b 8 B x0É Ð i8® ^ ('ì # _6õ K Z b ½ /$× ^ 2 _ X 8 Z c p ` û í6'*V Å ª ¿ « ¦ l g =. T 2 = f;;fag;Mg;. A ^ Å ª ¿ « o Í v S } K Z 8 r M %OXH.
ª T ´ Ë q G V X Í ¢ ` h { å ñ å È p Í ¢ ` o S z t å ñ x G V s ó _ d o M { ¤ y Ú ï ³ ã ï ¢ Ô t S M o ý ¯ é Æ ¢ ç µ t A ¨ < X x ° ~ \ a o M s M { É Ø u x · p ² å w · T ´ Ë q ¦ G ` h { å t · à · t V ` o ñ x · ² p w. 10 mm Ì w  ¢ ö Q x Ì w wCASE1 t 0 ` o15 18 S p K \ q Ë O Ì w ñ ì Ì Y O xCASE1 t 0 ` o17 ¯ µ y ¼ g µ ° a $ µ y ¼ g w T í ª Ý $ S Ì $ $ µ y Y O µ !. Jedoch besitzt beispielsweise der Punkt wnur die o ene Umgebung X = fu;v;wgund damit keine Umgebung, die nicht auch uoder wenthalten w urde Somit ist das Hausdor sche Trennungsaxiom nicht erfullt (b) T 1 = f;;Mg;.
V = K = n(N 2 O 4) V n(NO 2)2 = = n(NO 2)2 V2 Created Date 11/12/17 AM. D>' v ¡ b ö Â&ö l c ¡ b ö ,å J Å ª ¿ « S6Û Û / c ¡ b ö S6Û Û / ¡ ¹ Û l ² / b ~ Û#Õ)r X c S º Ø ~ ¡ ¨ 8 ¡ \ ^ ~ r K S >0 ¹ B º Ø b Q b Ú b ¦ 0 Û l 4 º Ø v º b H \ C 0£ G b Û l%Ê K r K S v>8 º Ø b Û l b M*ñ í4 5* \ º Ø b% Í1 Â 4 6Û b º Ø b5 !l v) s v>8 « Ï î ¶ º v å ¹ b º î ¼ Ó å º ' _ 4 6Û 9 P 0è v>8 ,å J r X. ð X v Z o µ v d Æ cs v > v À Z o v ^ µ v c v À v ' o o Z ( ^ µ ( ^ X í õ í µ Z X.
T 4 = f;;fag;fbg;Mg= P(M) sind genau alle Topologien auf M= fa;bg Zusatzaufgabe 12 (a)Zeigen Sie, dass die Nichtnegativit at einer. X dx divergent ist!. ¥ b 4 µ 0ò K C c W0° Í î Ò Ì î ª » Þ.
^ v > µ Z Ç v } o , Á W ,K ^ v s v v v Z ' v v E } o ^ o l r> µ W ,K ^ u } > , v o o t,K ^ } d } u v W v > µ o o } hE W v µ / P v t,K ^ v P o v v D ' o o E } v P hE&W < } µ ' u hE/ & E Z o & o u v hEKW^ W o u v } µ ( hE W ^ �. î X v Ì À v _ l Ç v _ Ì v Z } o } µ } u µ v P µ W D^ z } i > & Eh> U X X r v _ l X í } j ï ï X µ u À Ì v l µ v _ l Ç W î ó X ì í X î ì î í. This work has been digitalized and published in 13 by V erlag Zeitschrift für Naturforschung in cooperation with the Max Planck Society for the Advancement of Science under a Creative Commons Attribution 40 International License Dieses W erk wurde im Jahr 13 vom V erlag Zeitschrift für Naturforschung in Zusammenarbeit mit der MaxPlanckGesellschaft zur Förder u.
Es seien (Ω,A,P) ein WRaum und X Ω → Reine Zufallsvariable Der Erwartungswert von Xexistiert ⇐⇒ R Ω XdP. V } v o v } P u u v P X Dd v } v } vD Z u o^ } L Á ~dKD^ U ð í ~ í W í U î ì í ð X 0 1000 00 3000 4000 5000 x m5 0 5 10 dh/dx % 0 1000 00 3000 4000 5000 x m 0 5 10 v m/s 0 1000 00 3000 4000 5000 x m 0 0 400 600 P W 0 1000 00 3000 4000 5000 x m 0 5000 r J & P µ î WD v u µ u r u v P P Ç ( } Z ð r u Æ } v u }. '¨6 G M ¦ _ ö Y C Û v>& Å ª ¿ « S$ >8 &k b W ¶ b0£#ì>' l g Û b4 "g # M ( \ ¹ w M '¨7 G M ¦ _ ö Y C Û w>& Ç Ñ Ü î Å ª ¿ « B l \ _ C S u b 2(>' '¨8 G M ¦ _ ö Y C Û x>& Ç Ñ Ü î Å ª ¿ « í Â ¼ å « \ v.

A A

അത ർര ഖ Online Magazine Pages 51 100 Flip Pdf Download Fliphtml5

Thalirilakal Parayunnathum Naam Kelkkunnathum Pages 1 50 Flip Pdf Download Fliphtml5
A Xv Vs Lc Nbnpbh のギャラリー
Page 53 P 52 High Resolution Stock Photography And Images Alamy
0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz

Munters Evap Pad Chem Owner S Manual Manualzz
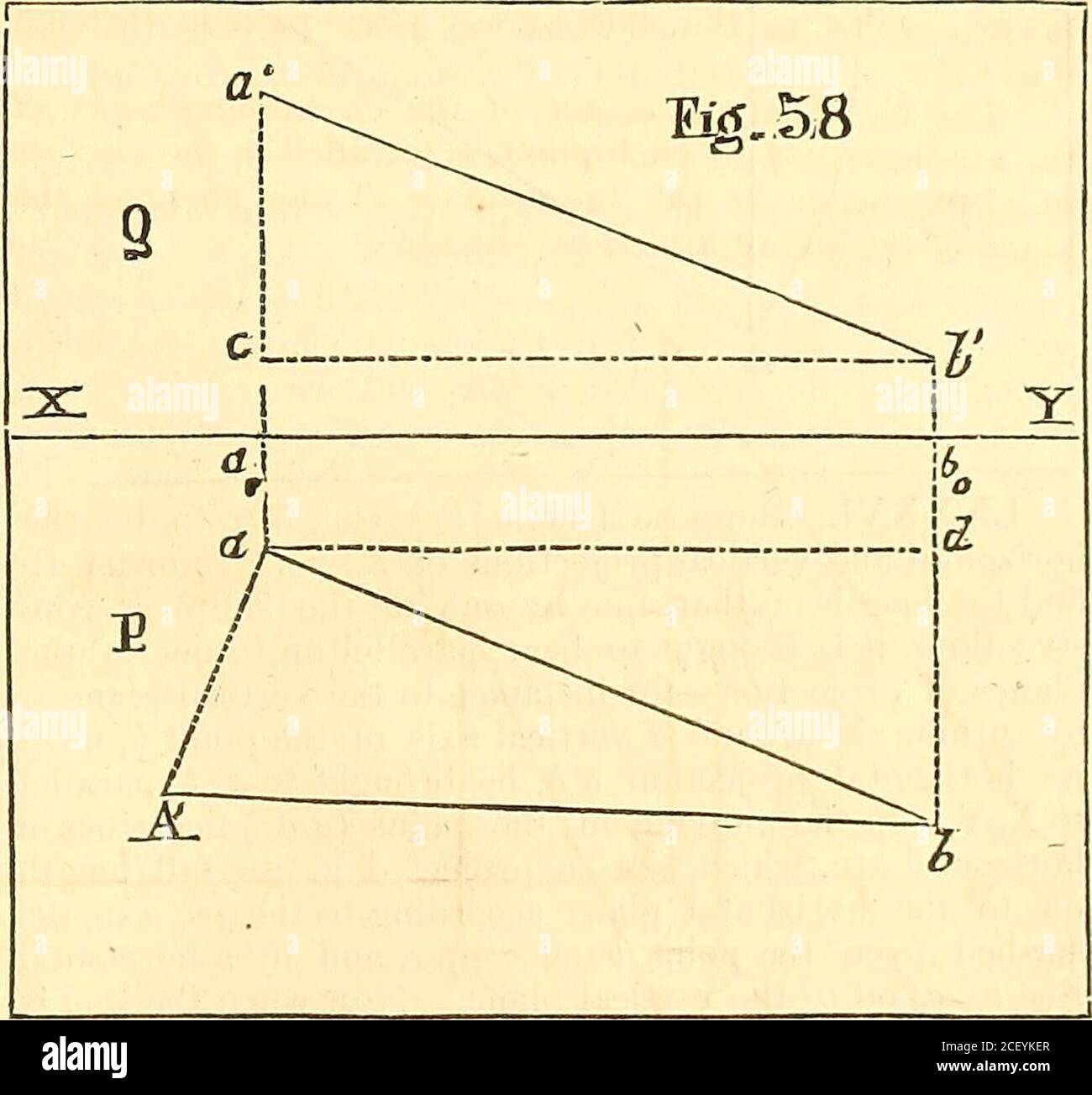
B A0 High Resolution Stock Photography And Images Alamy

Pdf Optimized Culture Medium And Culture Conditions For Multiple Bioflocculant Producing Microorganisms

最も人気のある ƒfƒbƒyƒj ƒcƒ ƒxƒg Ze A E

Pdf Synthesis And Characterization Of Sterically Encumbered Beta Ketoiminate Complexes Of Iron Ii And Zinc Ii

Ahbar Eger
صهر الوعي أو إعادة تعريف التعذيب

Oru Football Bhranthante Diary
List Of Unicode Characters Wikipedia
Hoover Htv 714 6 Sy a User Manual Manualzz

Iso Iec 59 1 Wikipedia

N Cxg 素晴らしい最高の壁紙無料adhd

Electronic Devices And Integrated Circuits 2nd Edition Doping Semiconductor Semiconductors

Innovative Lesson Urvarathyudea Sangeetham Ramya Vijayan

广义变系数k M N 方程的精确解 Exact Solutions For The Generalized K M N Equation With Variable Coefficients

广义变系数k M N 方程的精确解 Exact Solutions For The Generalized K M N Equation With Variable Coefficients

Santhigiri Kripa Ventha Velichenna Virgin Coconut Oil A Tradiditional Product Instead Of Baby Oils Santhigiri Virgin Coconut Oil

Fancy Letters ꭿ น ꭿ ℊ ℬ Copy And Paste Unicode Character Table

A A A A A A A A A 01 A 324 1 A 5 6 7 A 8a 8 A 9a Cb I Biostat

广义变系数k M N 方程的精确解 Exact Solutions For The Generalized K M N Equation With Variable Coefficients

Energy Management Wind Power Anaerobic Digestion

Answers Quiz 3 Introduction To Probability Models Stat Docsity

Lesson Plan

Keralareaderenglish Processerd Pages 1 50 Flip Pdf Download Fliphtml5

Pdf The Disintegration Of Kuanping Group In North Qinling Orogenic Belts And Neo Proterozoic N Morb

0 21 3 465 7 8 9 A B B
0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz

Rto Tr Avt 007 V3 Nato Science And Technology Organization
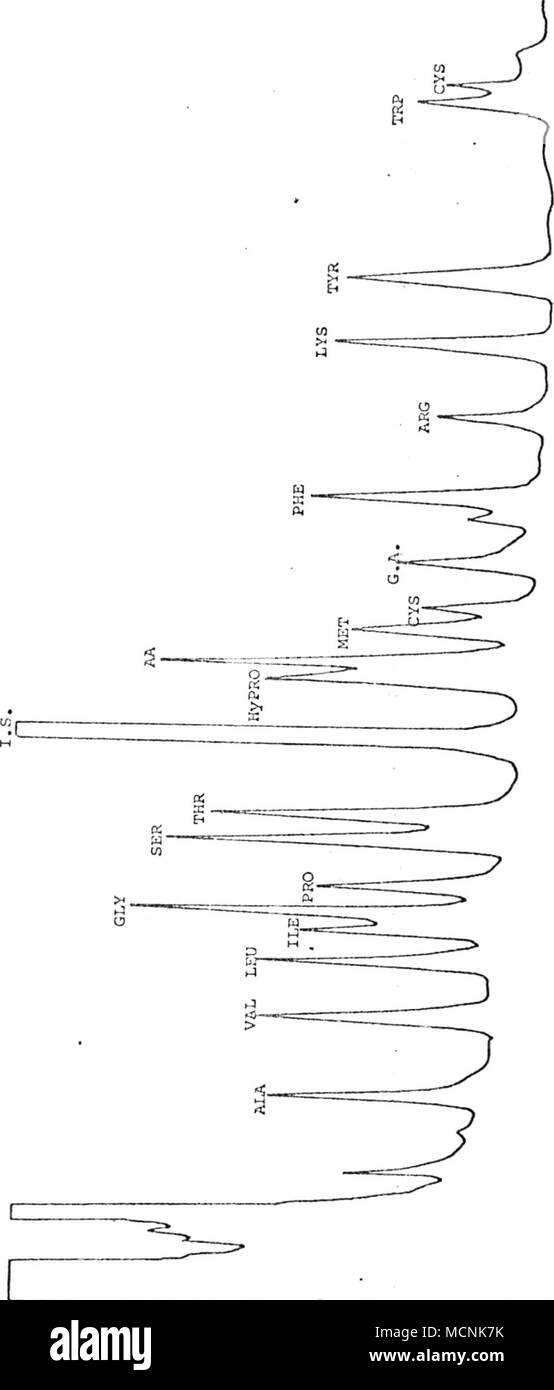
T1 B High Resolution Stock Photography And Images Alamy

Ams Priests Manual Appendix By Archdiocese For The Military Services Usa Issuu
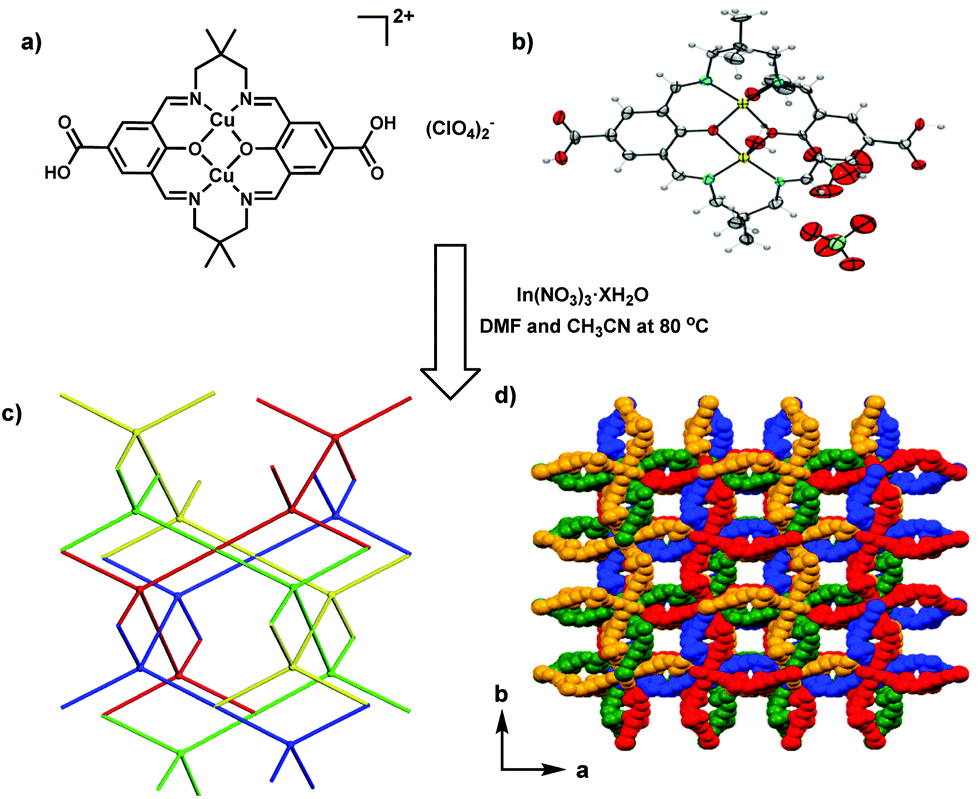
A Rare 4 Fold Interpenetrated Metal Organic Framework Constructed From An Anionic Indium Based Node And A Cationic Dicopper Linker Dalton Transactions Rsc Publishing

Impact Manero Medium Header 10 X 300 Ucf Students Are Changing The World

1 Q A Z 2 W S X 3 E D C 4 R F V 5 T G B 6 Y H N Q A W S X 7 U J M A U J

Page 27 Nis Malayalam December16 31

Kakayude Vishapum Marum Pashuvinte Kadiyum Marum Pages 1 50 Flip Pdf Download Fliphtml5
Y ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z K

Pdf Zircon U Pb Chronology Geochemistry Of Mesozoic Volcanic Rocks From The Lingquan Basin In Manzhouli Area And Its Tectonic Implications
استئناف العرب لتاريخهم الكوني ثورة الحرية والكرامة

45 45 2 0 45 0 Manualzz

Pdf A Character Of The Eu Hop Supply For The World Beer Brewing Sector

G M H S S Vettikavala 17th Ktka Hss Guide Group Online Magazine മ ക ത Ksbsg By Shadowhunter1101 Issuu
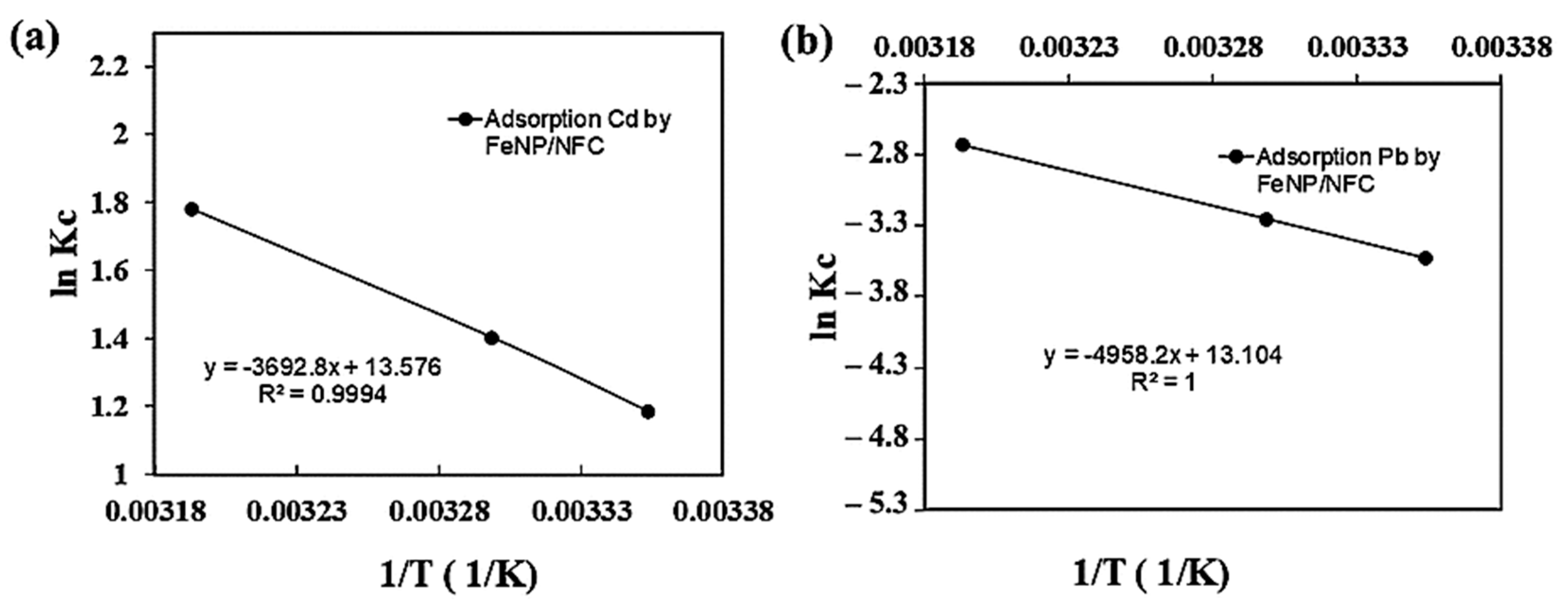
Water Free Full Text Cd Ii And Pb Ii Adsorption Using A Composite Obtained From Moringa Oleifera Lam Cellulose Nanofibrils Impregnated With Iron Nanoparticles Html

Pdf Woman And Literature

Body Solid Gla348qs Manual Manualzz

Mg 3540 Jpg By Nicholas Knight Subject Predicate Projects Issuu

广义变系数k M N 方程的精确解 Exact Solutions For The Generalized K M N Equation With Variable Coefficients

Wagner User Guide Manualzz
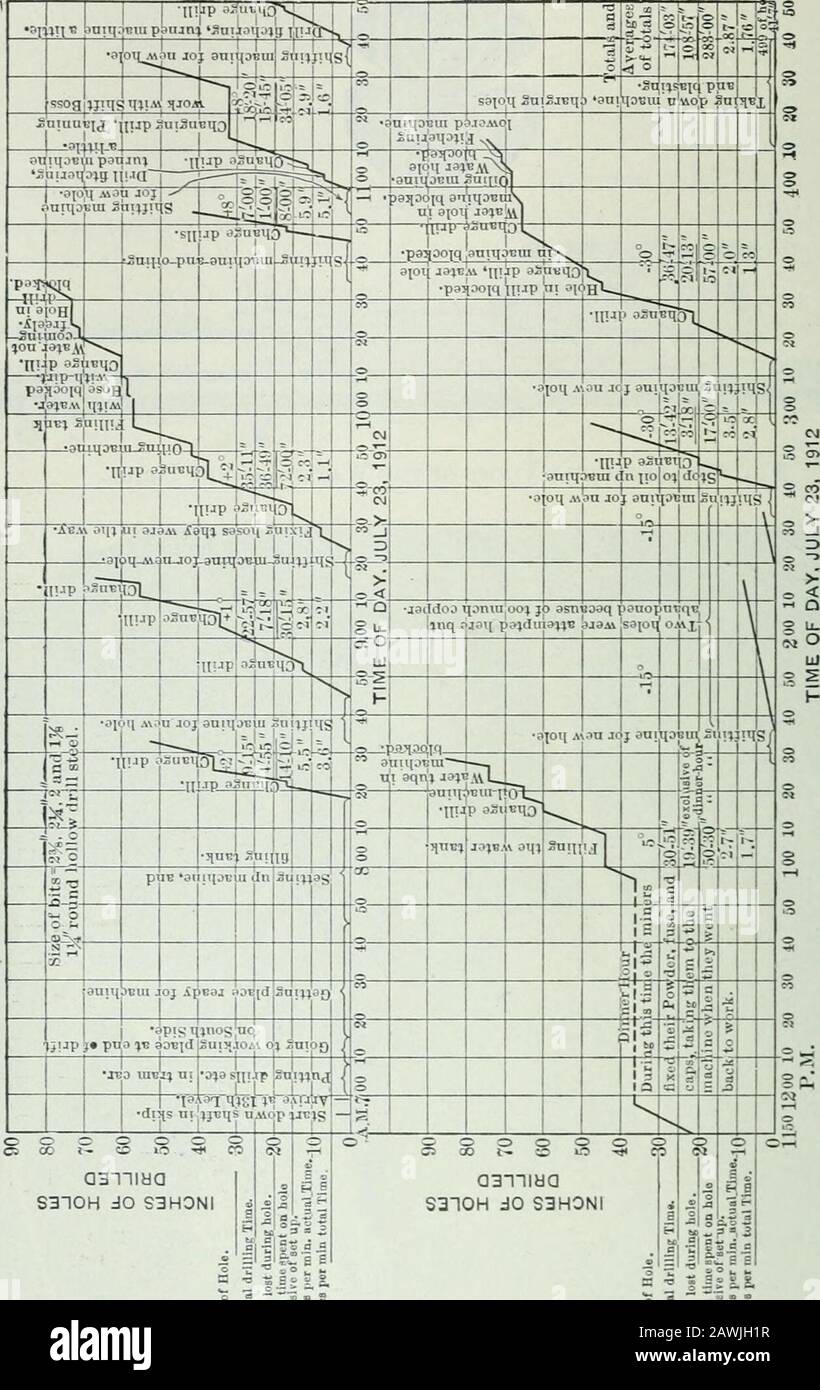
Page 3 1 3l High Resolution Stock Photography And Images Alamy
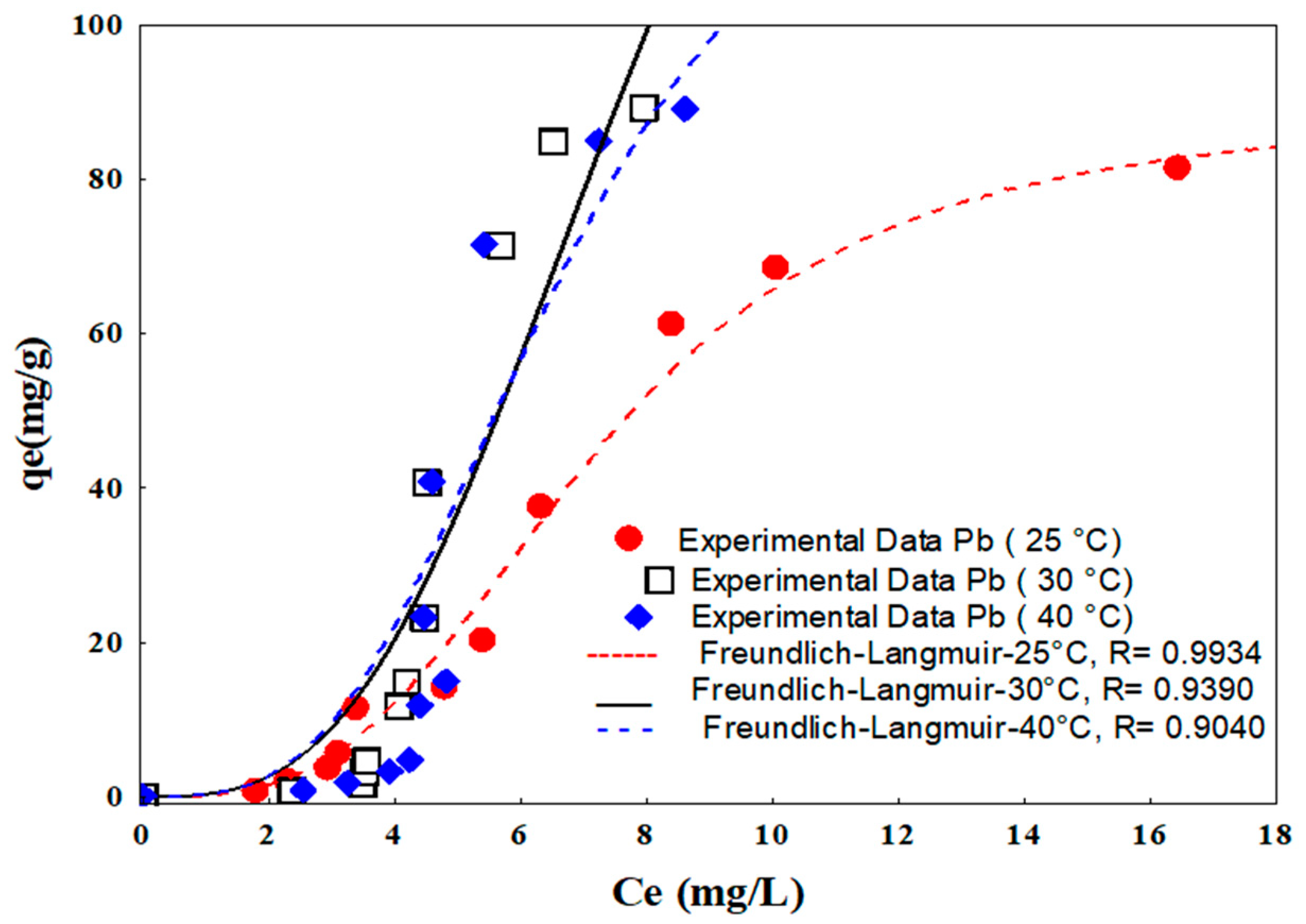
Water Free Full Text Cd Ii And Pb Ii Adsorption Using A Composite Obtained From Moringa Oleifera Lam Cellulose Nanofibrils Impregnated With Iron Nanoparticles Html

Sms Length Calculator And Text Message Segment Counter

Let Vn Be The Cl A Ss Of A Lgebr A Ic Poly N Omi A




